 Typical qubit gate operations are binary, involving operations with up to just two qubits. While this can be universal, it is more efficient for almost all quantum circuits to directly entangle qubits with N-body interactions. With trapped ions, gates are typically realized by applying optical state-dependent displacements to the ions. By instead using state-dependent squeezing forces, the workhorse quantum gate between pairs of trapped ions is extended to an N-qubit gate. This is an important shortcut for most quantum circuits such as quantum error-correction encoding and quantum optimization circuits, while also providing direct N-body interactions for quantum simulations of many-body quantum systems.
Typical qubit gate operations are binary, involving operations with up to just two qubits. While this can be universal, it is more efficient for almost all quantum circuits to directly entangle qubits with N-body interactions. With trapped ions, gates are typically realized by applying optical state-dependent displacements to the ions. By instead using state-dependent squeezing forces, the workhorse quantum gate between pairs of trapped ions is extended to an N-qubit gate. This is an important shortcut for most quantum circuits such as quantum error-correction encoding and quantum optimization circuits, while also providing direct N-body interactions for quantum simulations of many-body quantum systems.
- “Demonstration of three- and four-body interactions between trapped-ion spins,” Or Katz, Lei Feng, Andrew Risinger, Christopher Monroe, Marko Cetina, Nature Physics 19, 1452 (2023); arXiv:2209.05691.
- “Programmable N-body interactions with trapped ions,” O. Katz, M. Cetina, and C. Monroe, Phys. Rev. X Quantum 4, 030311 (2023); arXiv:2207.10550.
- “N-body interactions between trapped ion qubits via spin-dependent squeezing,” O. Katz, M. Cetina, and C. Monroe, Phys. Rev. Lett. 129, 063603 (2022).



![Encoding and stabilizer readout schematic for the Bacon-Shor [[9,3,1]] error correction process.](https://iontrap.duke.edu/files/2021/10/FTQEC-1024x331.jpg)

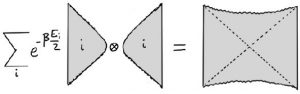

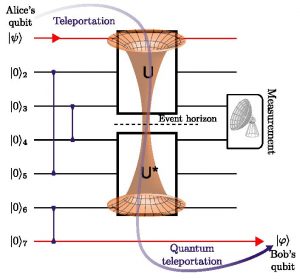

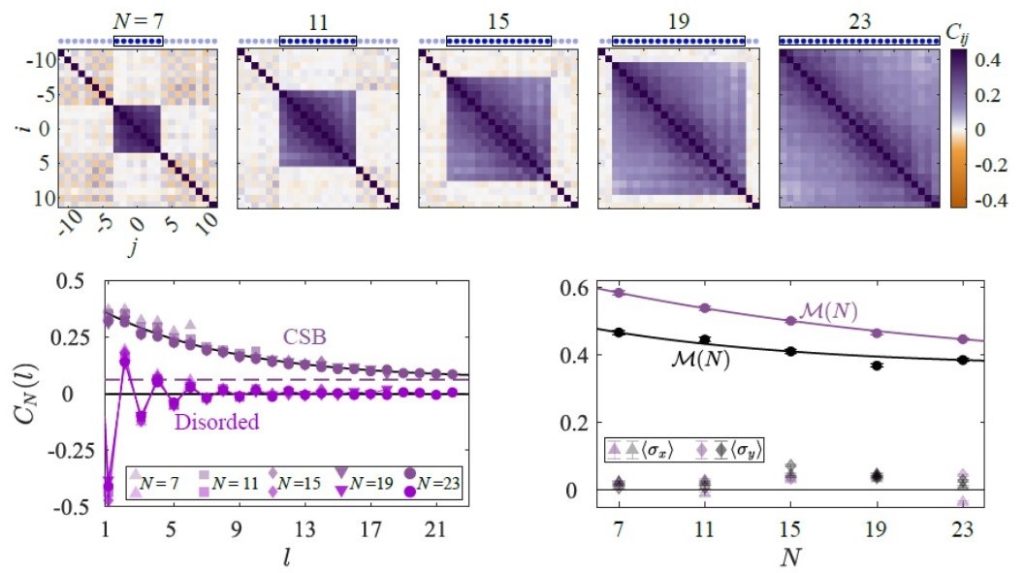
 In one of the largest quantum simulations ever performed, up to 53 trapped ion qubits have been used to simulate properties of many body magnetic interactions. The qubits are each prepared with individual control, and measured in a single shot with nearly 100% efficiency. This allows the observation of arbitrary correlation functions that cannot be calculated. This restricted quantum computer becomes fully programmable and reconfigurable with straightforward modifications in the control lasers.
In one of the largest quantum simulations ever performed, up to 53 trapped ion qubits have been used to simulate properties of many body magnetic interactions. The qubits are each prepared with individual control, and measured in a single shot with nearly 100% efficiency. This allows the observation of arbitrary correlation functions that cannot be calculated. This restricted quantum computer becomes fully programmable and reconfigurable with straightforward modifications in the control lasers.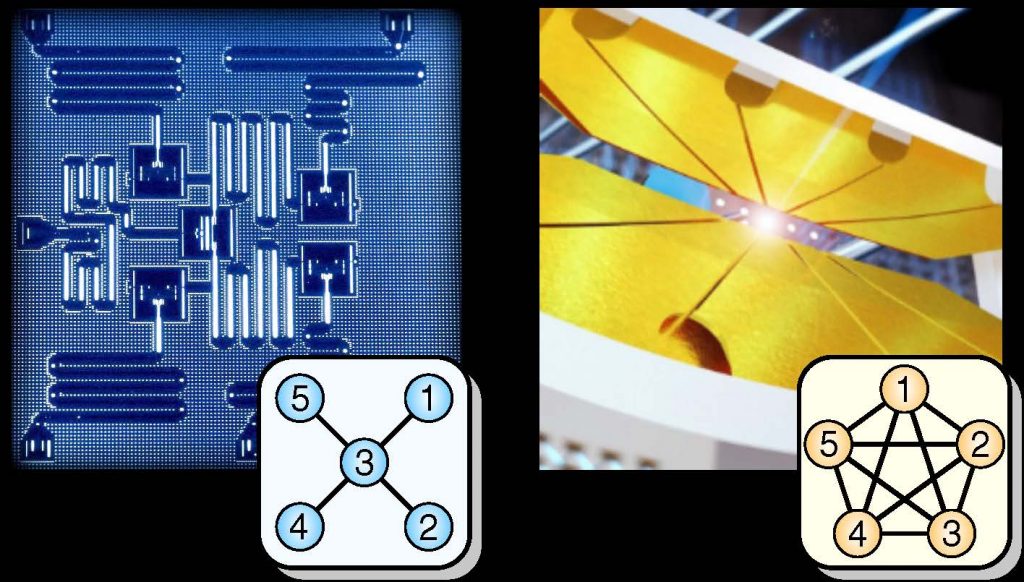 Connectivity between qubits in a quantum computer may be as important as clock speed and gate fidelity when it comes time to build large-scale quantum computers. We run several quantum algorithms on two 5-qubit programmable quantum computers:
Connectivity between qubits in a quantum computer may be as important as clock speed and gate fidelity when it comes time to build large-scale quantum computers. We run several quantum algorithms on two 5-qubit programmable quantum computers: 